MEX Tree codeforces solution 2021
SOLUTION
” CLICK HERE “
You are given a tree with nodes, numerated from to . For each between and , inclusive, you have to count the number of unordered pairs , , such that the MEX of all the node labels in the shortest path from to (including end points) is .
The MEX of a sequence of integers is the smallest non-negative integer that does not belong to the sequence.
The first line contains a single integer () — the number of test cases.
The first line of each test case contains a single integer ().
The next lines of each test case describe the tree that has to be constructed. These lines contain two integers and () denoting an edge between and ().
It is guaranteed that the given edges form a tree.
It is also guaranteed that the sum of for all test cases does not exceed .
For each test case, print integers: the number of paths in the tree, such that the MEX of all the node labels in that path is for each from to .
2 4 0 1 0 2 2 3 2 1 0
1 2 1 1 1 0 0 1
- In example case ,
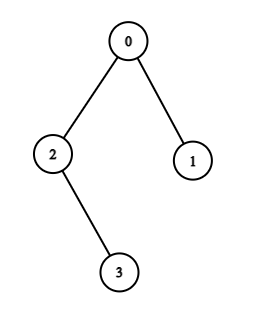
- For , there is path that is from to as .
- For , there are paths that is from to as and to as .
- For , there is path that is from to as .
- For , there is path that is from to as
- For , there is path that is from to as .
- In example case ,
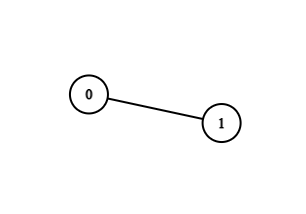
- For , there are no such paths.
- For , there are no such paths.
- For , there is path that is from to as .


![[SOLUTION] Group Sum Solution Codchef - The positive even numbers are sorted in ascending order as 2, 4, 6, 8, 10, 12, 14, 16 ……, and grouped as (2), (4, 6), (8, 10, 12), (14, 16, 18, 20) and so on](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEivZ5Sv6AgukYAkJMuqiVtgHqBkPBSjVR3oL3OdiYEOcDG6dwejzEc6rsb_6u6GdUmHmBStNqgs_hZf8pJtA5DAYN75ypzQ_WK9tWOJY6m2vCZVuvZzeGXUe47c6sqY6TdMFt0PWLVGI0NB/w72-h72-p-k-no-nu/20210413_190651.png)
Social Plugin